Logisztikus regresszió 1. rész — modell készítése

A mai bejegyzésben egy népszerű osztályozó modellt fogunk megismerni. Alapesetben két csoport modellezésére szokták használni, de ki lehet terjeszteni több csoportra is.

A logisztikai regressziót már említettem korábban a ROC görbe alatti területről szóló bejegyzés során. Ott elhangzott, hogy a kimenete annak a valószínűsége, hogy egy megfigyelés egyik vagy másik csoportba tartozik e. Hogy megértsük a működését, ennek a tételnek a naiv megfogalmazásával kell kezdenünk. De először kezdjük a szokásos példa adatokkal.

Példa adatok

A korábban már sokszor használt Szélerősség és “Esni fog 2 órán belül” adatokat fogjuk most is használni:

	Független változó	Függő változó
Sorszám (i)	Szélerősség (km/óra)	Esni fog 2 órán belül
1	3,5	Igen
2	3,2	Nem
3	1,5	Igen
4	3,6	Nem
5	0,2	Igen
6	0,1	Igen
7	0,2	Nem
8	0,4	Igen
9	0,4	Igen
10	0,2	Nem

Teszt adatok

A Logisztikus regresszió alapesetben egy esemény/állapot fennállását vagy hiányát modellezi. Így a függő változónkat 0 és 1 értékeként kell ábrázolunk, ahol 1 amikor az esemény bekövetkezik és 0 amikor nem. Ennek megfelelően kódoljuk át az “Esni fog 2 órán belül” változónkat:

	Független változó	Függő változó
Sorszám (i)	Szélerősség (km/óra)	Esni fog 2 órán belül
1	3,5	1
2	3,2	0
3	1,5	1
4	3,6	0
5	0,2	1
6	0,1	1
7	0,2	0
8	0,4	1
9	0,4	1
10	0,2	0

Teszt adatok

Most, hogy a mintaadataink készen vannak, nézzük meg a valószínűség fogalmát egy kicsit más szempontból.

Esély és valószínűség

A klasszikus elméletben a valószínűség kiszámításához annak valószínűségét kell kiszámítani, hogy valami megtörténik. A valószínűség egy tört, ami kifejezi, hogy valami megtörténik az összes lehetséges esemény közül. A fenti példánál maradva annak a valószínűsége, hogy esni fog két órán belül:

$p = \frac{\sum_{i=1}^n \text{y}_i}{n} = \frac{6}{10}$

Ahol:

p — a valószínűség
i — sorszám
n — mintanagyság, jelen példánál 10
y — az esemény, jelen példánál “Esni fog 2 órán belül”

A mindennapi életben erre azt mondnánk, hogy 60% a valószínűsége az esőnek. Van viszont egy másik eljárás is a bizonytalanság számszerűsítésére, ez az esély (angolul: odds). Az esélyt a sportfogadások során szokták leginkább használni a mindennapokban. Ez annak az aránya, hogy valami megtörténik vs. nem történik meg. A fenti példa esetén mennyi alkalommal esik? 6. És mennyi amikor nem esik? 4. Vagyis az “Esni fog 2 órán belül” esélye:

$esely = \frac{6}{4}$

Az esélyt a valószínűségből is ki lehet számítani. Ugye a valószínűség megadja mennyiszer következik be valami, és ha ezt kivonjuk a 1-ből (a teljes valószínűségből), akkor megkapjuk mennyiszer nem történik meg egy esemény:

$esely = \frac{p}{1-p}$

Logit függvény

Az egyik probléma az Eséllyel, hogy nem szimmetrikus. A 6:4 és a 4:6 nem egyforma távolságra van az 1-től (ugye 1, amikor valami egyforma esélyek bekövetkezik vagy elmarad):

Ezen segít a logaritmus:

$\left| \log\left( \frac{6}{4} \right) \right| = \left| \log\left( \frac{4}{6} \right) \right|$

Ezzel meg is érkeztünk a logisztikus regresszió egyik kulcs fogalmához a logit függvényhez:

$\text{logit}(p) = \log\left( \frac{p}{1-p} \right)$

Mi jellemzi ezt a függvényt? Gondolom senkit sem lep meg, hogy a minimuma minusz végtelen:

$\text{logit}(p=0) = \log\left( \frac{0}{1-0} \right) = \log(0) = -\infty$

Mi a maximuma? Pozitív végtelen. Ez talán annyira nem egyértelmű, így vizsgáljuk meg ezt egy kicsit közelebbről. Az elég egyértelmű, hogy minél gyakrabban megtörténik valami, annál nagyobb az Esélye, vagyis monoton növekszik. De mi van ha minden egyes alkalommal esik? Ekkor az esély:

$\text{logit}(p=1) =\log\left( \frac{1}{1-1} \right) = \log\left( \frac{1}{0} \right)$

De ugye 0-val nem osztunk. Szerencsére itt logaritmus van, így megtehetjük, hogy átírjuk:

$\text{logit}(p=1) = \log(1)-\log(0)$

Mivel $\log(0) = -\infty$ és “valami-(-végtelen) = +végtelen”:

$\text{logit}(p=1) = \infty$

Mi történik, ha ezt a logit függvényt a függő változónkon fogjuk használni? Értelemszerűen mínusz és plusz végtelenben toljuk ki az értékeket:

	Független változó	Függő változó
Sorszám (i)	Szélerősség (km/óra)	logit(Esni fog 2 órán belül)
1	3,5	∞
2	3,2	-∞
3	1,5	∞
4	3,6	-∞
5	0,2	∞
6	0,1	∞
7	0,2	-∞
8	0,4	∞
9	0,4	∞
10	0,2	-∞

Logit adatok

Ezt ábrázolhatjuk is:

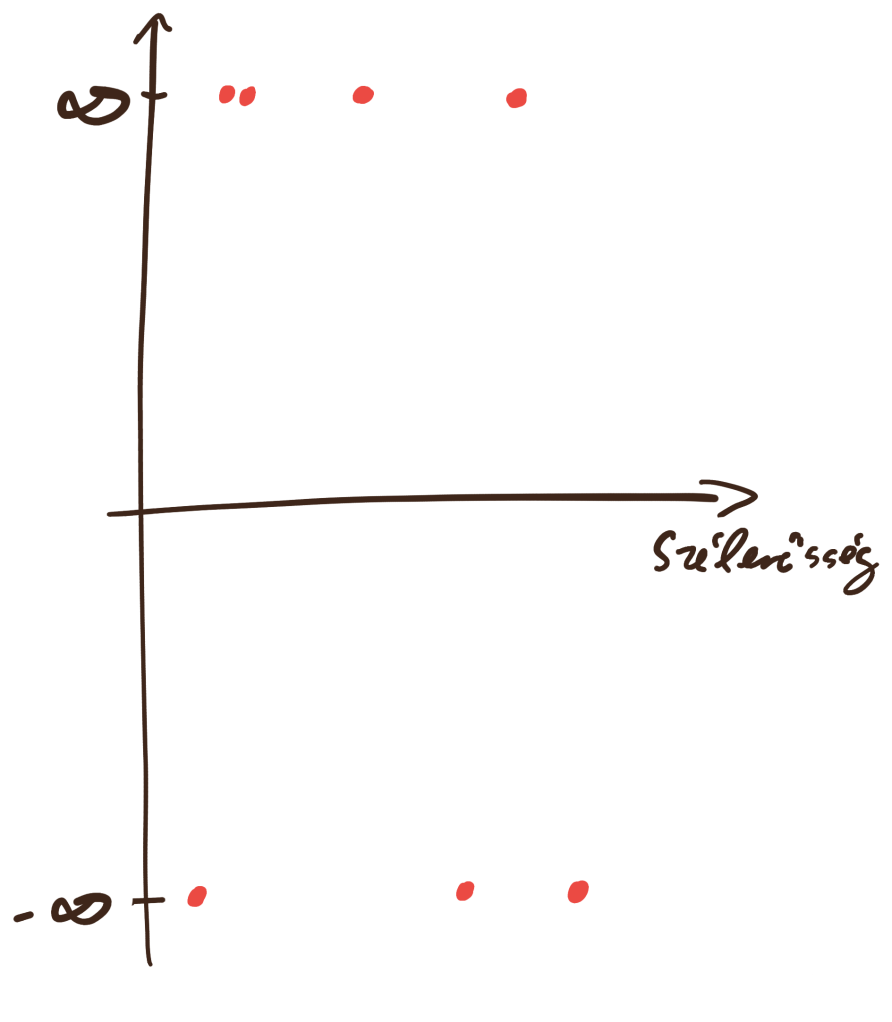
Ezt elég kényelmetlen ábrázolni, de ez lesz a Logisztikus regresszió modell tanuló adatai. Ugye a probléma ami itt fennáll az, hogy az logit(“Esni fog 2 órán belül”) értékei a végtelenben vannak, így pedig nem lehet Loss függvényt számolni: Minden modell esetén végtelen lesz a modell és a megfigyelések távolsága. Lássuk, hogy kezeli ezt a problémát a logisztikus regresszió.

Legnagyobb valószínűség

Bár a Loss függvényt nem lehet alkalmazni, de a legnagyobb valószínűséget (angolul: maximum likelihood) igen. Hogyan? Ugye fentebb már láttuk, hogy az log(esély) kiszámítható a valószínűségből:

$\text{logit}(p) = \log(esely) = \log\left( \frac{p}{1-p} \right)$

Ezt meg is lehet fordítani és a log(esély)-ből is kiszámíthatjuk a valószínűséget. Először emeljük mint két oldal az e hatványára:

$e^{\log(esely) } = \frac{p}{1-p}$

Ezután már csak egy kis átrendezés kell:

$(1-p) \cdot e^{\log(esely) } = p$

$e^{\log(esely) }-p\cdot e^{\log(esely) } = p$

$e^{\log(esely) }= p + p\cdot e^{\log(esely) }$

$e^{\log(esely) } = p\cdot (1+e^{\log(esely) } )$

$\frac{e^{\log(esely) }}{1+e^{\log(esely) }} = p$

Fordítsuk meg:

$p = \frac{e^{\log(esely) }}{1+e^{\log(esely) }}$

Rendben tehát el tudunk jutni az esélytől a valószínűségig és vissza. Most már csak egy modell kell. A logisztikus regresszió igazából egy lineáris regresszió, ahol az esély logaritmusa a függő változó:

$f(x) = \alpha + \beta \cdot x$

Ábrázolva:

Mi lesz a legnagyobb valószínűség ennél a modellnél? A modellre vetített megfigyelések valószínűségének szorzata:

$L = \prod_{i:y=1} \left( p \right) \cdot \prod_{i:y=0} \left( 1-p \right)$

Amit felírhatunk az esélyel is:

$L = \prod_{i:y=1} \left( \frac{e^{f(x)}}{1+e^{f(x)}} \right) \cdot \prod_{i:y=0} \left( 1- \frac{e^{f(x)}}{1+e^{f(x)}} \right)$

Ez talán első re bonyolultnak tűnik de nem az. Nézzük meg közelebbről! Az első szorzat azok az esetek, amikor 1 az osztály változónk értéke. A fenti példánál amikor esik. A második szorzat pedig azok az esetek, amikor 0 az osztály változón, vagyis amikor nem esik. Miért tér el a két számítás? Mert a esély az az esemény bekövetkeztének lehetőségét méri, ha a nem bekövetkeztét szeretnénk mérni, akkor ezt ki kell vonnunk a teljese valószínűségből, ami ugye 1.

Mit tudunk erről az értékről? Minél nagyobb a modellünk annál valószínűbb. És itt meg is érkezünk a logisztikus regresszió algoritmus lényegéhez: megtalálni azt a modellt ami maximalizálja a legnagyobb valószínűséget az esély logaritmusán. Bár ez önmagában elég is, a gyakorlati életben a legnagyobb valószínűséget logaritmusát szokták maximalizálni. Miért? A logaritmus ugye a szorzást összeadássá alakítja, és ezt hatékonyabb számolni. Vagyis a következő kifejezést fogja az algoritmus maximalizálni:

$ll = log(L) = \sum_{i:y=1} \log\left( \frac{e^{f(x)}}{1+e^{f(x)}} \right) + \sum_{i:y=0} \log\left( 1- \frac{e^{f(x)}}{1+e^{f(x)}} \right)$

Vagy esélyel felírva:

$ll = log(L) = \sum_{i:y=1} \log\left( p \right) + \sum_{i:y=0} \log\left( 1- p \right)$

Példa számítás

Legyen a modellünk a következő:

$y = f(x) = 0{,}2 + 0{,}06 \cdot x$

Számítsuk ki az első megfigyelés valószínűséget az adott modellre:

$\log(\text{esely})_1 = 0{,}2 + 0{,}06 \cdot \text{szelerosseg }$

$\log(\text{esely})_1 = 0{,}2 + 0{,}06 \cdot 3{,}5 = 0{,}41$

$p_1 = \frac{e^{\log(esely)_1 }}{1+e^{\log(esely)_1 }} = \frac{e^{0{,}41}}{1+e^{0{,}41}} \approx 0{,}601$

Most a másodikra:

$\log(\text{esely})_2 = 0{,}2 + 0{,}06 \cdot 3{,}2 = 0{,}392$

$p_2 = 1- \frac{e^{\log(esely)_2 }}{1+e^{\log(esely)_2 }} = 1 - \frac{e^{0{,}392}}{1+e^{0{,}392}} \approx 0{,}403$

Minden pontra:

	Független változó	Függő változó
Sorszám (i)	Szélerősség (km/óra)	logit(Esni fog 2 órán belül)	p(x_i)	log(p(x_i))
1	3,5	∞	0,601	-0,509
2	3,2	-∞	0,403	-0,908
3	1,5	∞	0,572	-0,559
4	3,6	-∞	0,397	-0,923
5	0,2	∞	0,553	-0,593
6	0,1	∞	0,551	-0,595
7	0,2	-∞	0,447	-0,805
8	0,4	∞	0,556	-0,587
9	0,4	∞	0,556	-0,587
10	0,2	-∞	0,447	-0,805
Log legnagyobb valószínűség (l)				-6,871

Log legnagyobb valószínűség

Ezzel lényegében készen is vagyunk. Most már csak egy algoritmus kell, ami kipróbál egy rakás lehetséges lineáris modellt és kiválasztja ezek közül azt, aminél a legnagyobb lesz a valószínűség.

Python példakód

Most, hogy tudjuk miként választjuk ki a legjobb modellt a logisztikus regresszió algoritmusa, nézzünk egy példa Python kódot:

import numpy as np
from statsmodels.api  import Logit
import statsmodels.api as sm

adatok = np.array([
              [3.5, 1],
              [3.2, 0],
              [1.5, 1],
              [3.6, 0],
              [0.2, 1],
              [0.1, 1],
              [0.2, 0],
              [0.4, 1],
              [0.4, 1],
              [0.2, 0]
           ])

y = adatok[:, 1]
# egy Konstans + Szélerősség  
X = sm.add_constant(adatok[:, 0])
log_reg = Logit(y, X).fit()
log_reg.summary()

Ami eredménye:

Logisztikus regresszió statsmodels eredmény

Mint látható a legjobb modell:

$f(x) = 0{,}9378 - 0{,}3841 \cdot x$

Ábrázoljuk a modellt:

import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (10,7)

def xcalc(p, alfa, beta):
    return (np.log((p/float(1-p)))-alfa)/beta

plt.clf()
# modell 0,05 és 0,95 valószínűség között
minimum = xcalc(0.05, log_reg.params[0], log_reg.params[1])
maximum = xcalc(0.95, log_reg.params[0], log_reg.params[1])
X_test = np.linspace(minimum, maximum, 100)
hatar = xcalc(0.5, log_reg.params[0], log_reg.params[1])
X_test = sorted(np.concatenate(([hatar], X_test)))
# add constant
X_test = sm.add_constant(X_test)
p_test = log_reg.predict(X_test)
plt.plot(X_test[:, 1], p_test, label="Modell")
# megfigyelések
plt.scatter(adatok[:, 0],adatok[:, 1], color="black", label="megfigyelések" )
# területek
szurt_x = [ x for x in X_test[:, 1] if x >= hatar ]
plt.fill_between(szurt_x, 
                 p_test[len(szurt_x)-1:], 
                 [ -0.1 for x in szurt_x], 
                 alpha=0.5, color='#539ecd', label="Valós negatív")
szurt_x = [ x for x in X_test[:, 1] if x < hatar ]
plt.fill_between(szurt_x, 
                 p_test[:len(szurt_x)], 
                 [ 1.1 for x in szurt_x], 
                 alpha=0.5, color='#87CEFA', label="Valós pozitív")
# határ
plt.axvline(hatar, label=f"határérték: {np.round(hatar, 2)}", color="orange")

plt.legend()
plt.xlabel("Szélerősség")
plt.ylabel("Valószínűség")
plt.show()

Ami eredménye:

Befejezés

A következő bejegyzésben megnézzük, hogy válasszuk ki a legjobb modellt. Ehhez megtárgyaljuk a determinációs együttható és a p-érték számítását logisztikus regresszióra.

Vélemény, hozzászólás? Kilépés a válaszból

Hozzászólás

Adatok megadása vagy bejelentkezés valamelyik ikonnal:

E-mail cím (Nem lesz látható)

Név

Honlap

Hozzászólhat a WordPress.com felhasználói fiók használatával. ( Kilépés / Módosítás )

Hozzászólhat a Facebook felhasználói fiók használatával. ( Kilépés / Módosítás )

Kilépés

Kapcsolódás: %s

Példa adatok

Esély és valószínűség

Logit függvény

Legnagyobb valószínűség

Példa számítás

Python példakód

Befejezés

Share this:

Tetszett a bejegyzés?

Kapcsolódó bejegyzések

Közzétéve: sajzsoltattila

Vélemény, hozzászólás? Kilépés a válaszból