Mai bejegyzésünkben a Döntési fa egyik továbbfejlesztését fogjuk megismerni: a Véletlenszerű Erdőt (angolul: Random Forest). A korábbi bejegyzésben említettem, hogy a Döntési fa bizonyos esetekben könnyen túlilleszthető. Ennek megakadályozására az előző bejegyzésben paraméterekkel láttuk el az algoritmust, ami magával hozza a paraméter optimalizációs problémákat. A Véletlenszerű erdő a Döntési fák túlillesztési problémáját általánosabban közelíti meg.
A Véletlenszerű erdő első algoritmusát 1995 publikálta Tin Kam Ho. Ezt Leo Breiman és Adele Cutler továbbfejlesztette, majd 2006-ban védjegyet is jegyeztek be a “Random Forest” elnevezésre.
A Véletlenszerű erdő az Együttes (angolul: Ensemble) módszerek egyik változata, így először erről kell egy kicsit beszélnünk.
Együttes módszer
Valószínűségi modellekkel dolgozni mindig bizonytalanságot jelent, ezért valószínűségiek ugye. Az is gondolom nyilvánvaló, hogy nem létezik a Gépi tanulás Szent Grálja (vagy legalábbis eddig nem találták meg). Az Együttes módszer ebből a két állításból indul ki, és egy triviális választ add arra a problémára, hogy a modelljeink valamilyen szinten mind rosszak: Használjunk több modellt és kombináljuk őket. Kb. mint ha az Amadinda Együttes csinálna gépi tanulást: Mindenki ugyanazon a hangszeren játszik, de mást-mást. Mégis az eredmény együtt lesz egész. A blogon már volt szó egy ilyen módszerről: a Dropoutról. Ott súlyok véletlenszerű dobásával állítunk elő különböző típusú modelleket. A Véletlenszerű Erdő egy másik, bagging-nek (az angol „bootstrap aggregating” rövidítése. A „bootstrap” a cipő vagy a csizma húzóját, fülét jelenti. Az elnevezés a saját erőből történő problémamegoldásra biztató és a „Pull yourself up by your own bootstraps!” angol mondásból származik.) nevezett módszert használ. Nézzük meg mi ez.
Bagging
A módszer a modell átlagolás (model averaging) nevű stratégiák közé tartozik, amelyek alapötlete, hogy több osztályozót tanítunk egymástól elkülönítve. A különböző osztályozókat úgy készítjük, hogy ugyanazt az algoritmust különböző visszatevéssel véletlenszerűen választott adatokkal tanítjuk. Az így kialakított modellek egyenként kevésbé lesznek pontosak mint egy osztályozó, ami az összes adatot megtanulta. De mi pont ezt szeretnénk a túlillesztés elkerülése végett. Amikor egy új bemenet osztályáról kell dönteni, akkor ezek a modellek szavaznak, és a többségi szavazás eredményének megfelelő címkét rendeljük a bemenethez.
Gondolom most már érthető miért Véletlenszerű Erdő a módszer neve. Erdő mert több (Döntési) Fából épül fel, és Véletlenszerű, mert az egyes Fák és velük az egész Erdő véletlenszerűen válogatott adatokkal tanított.
Ami érdekes, hogy a módszer az egyes új megfigyelések osztályának bizonytalanság mérésére is alkalmas. Ehhez csak tárolnunk kell a megfigyelés esetén minden egyes osztályt, amire szavazat érkezett.
Nézzünk erre egy példát a Döntési fa tanítása során megismert adatokon. Első lépésben más-más adatokkal létrehozunk több fát:
A tesztelés során a fentebb létrehozott összes fa megkapja az új megfigyeléseket és szavaznak róla. A legtöbb szavazatot kapott kimeneti osztály lesz a győztes:
Véletlenszerű erdő
A véletlenszerű erdő a fenti bagging eljárást kiegészíti egy másik hasonló eljárással: a független változók mintavételével. Mi is ez? Mint láttuk az egyszerű bagging esetén sorokat választunk ki véletlenszerűen. Itt nem csak sorokat, hanem független változókat is. Miért? Az egész Együttes módszer lényege, hogy a részmodelljeink egymástól minél függetlenebbek legyenek. Minél inkább korrelálnak, annál inkább nem csinálunk semmi mást csak másolgatjuk ugyanazt a fát. Ha így teszünk, akkor pedig nem oldjuk meg az eredeti problémát, hanem csak megsokszorozzuk. Ho azt vette észre, hogy a korráció a Döntési fa modellek között nem csak a tanulási mintáktól függ, hanem a tulajdonságoktól is. Ha van néhány független tulajdonság, ami jól magyarázza a függő tulajdonságot, akkor azok több fában is dominánsak lesznek. Ez pedig hasonló modellekhez fog vezetni, amit meg nem szeretnénk.
Nézzük meg ezt korábban megismert adatokon ezt a mintavételt:
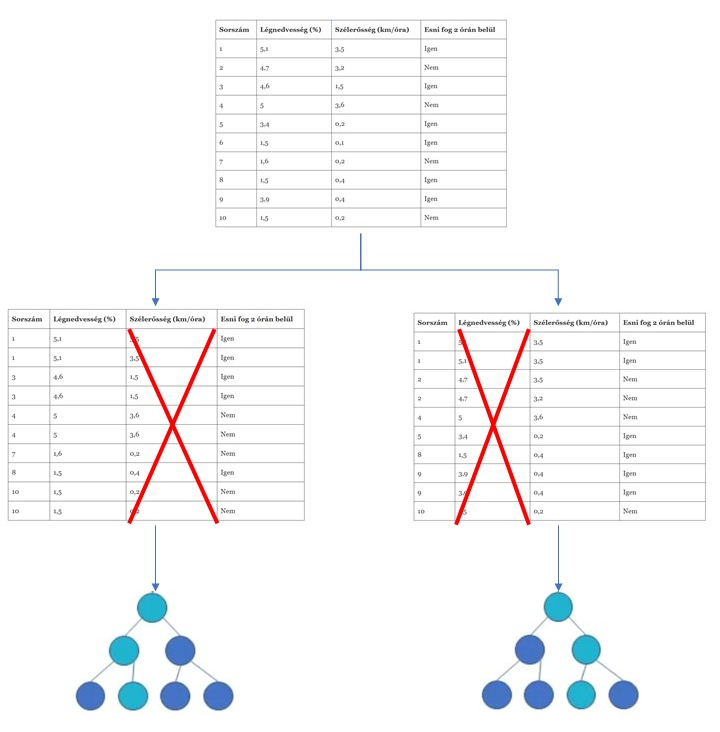
A fenti példában az első fánál a Légnedvességet dobtuk, a másodiknál pedig a Szélerősséget. Gondolom elég egyértelmű, hogy ez a módszer változatosabb fákat hoz létre, mints a bagging.
Egy kérdést kell még megvizsgálnunk: mennyi tulajdonságot használjunk fel a fák tanításához. Erre nincs egyértelmű szabály, a bevett gyakorlat, a 
A Véletlenszerű Erdő megismerése után a következő bejegyzésben egy másik a Döntési fán alapuló modellt fogunk megismerni az XGBoost-ot.
Irodalom
- IBM — Random Forest
- Szabó Dániel — Gépi tanulás és kvantuminformatika
Sajó Zsolt Attila 